本篇旨在帮助开发人员回顾在 2D 图形编程中可能会涉及到的数学知识。

矩形

矩形面积 $S = 长 * 宽$

矩形周长 $C = 2 * ( 长 + 宽)$

两点间的距离

在直角坐标系中，设两个点 A、B 以及坐标分别为$A(x1,y1)$ 、$B(x2,y2)$ ，则 A 和 B 两点之间的距离为：

$\left | AB \right |=\sqrt{ {(x1-x2)}^2 + {(y1-y2)}^2 }$

圆

通常使用$r$表示圆的半径；

圆的面积 $S = {\pi}r^2$

圆的周长 $C = 2{\pi}r$

当圆心坐标为(0，0)时，圆的方程式为：

$x^2 + y^2 = r^2$，表示的曲线是以 O(0，0)为圆心，以 r 为半径的圆。

当圆心坐标不为(0，0)时，圆的方程式为：

$(x - a)^2 + (y - b)^2 = r^2$ 表示的曲线是以 O(a，b)为圆心，以 r 为半径的圆。

弧度与角度

弧度是基于圆的半径的纯计量单位，当角度以弧度给出时，通常不写弧度单位，或有时记为rad。

弧度是指在一个圆中，弧长和半径之比，即：$\left | 弧度 \right |=弧长\div半径$。

我们知道，一个圆的周长为 $2{\pi}r$，所以可得一个圆的弧度为 $\frac{2{\pi}r}{r}=2\pi$

已知一个圆的角度是$360^{\circ}$，所以 $360^{\circ}==2{\pi}$

由此可知二者转换关系为：

$1^{\circ} =\frac{\pi}{180} rad$

$1 rad = (\frac{180}{\pi})^{\circ}$

三角形

若三角形的三边分别为 a，b，c，其中 c 为底边，高为 h，三角分别为 A（$\alpha$），B（$\beta$），C（$\gamma$），如下图所示，在 △ABC 中

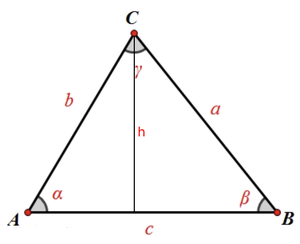
面积 $S = \frac{1}{2} ch$

周长 $C = a + b + c$

三角形的三个角相加永远是 $180^{\circ}$，即 $\alpha+\beta+\gamma=180^{\circ}$，因此等边三角形的每个角都是 $60^{\circ}$

正弦/余弦/正切

正弦、余弦和正切是基于直角三角形而建立的。

$\sin(\theta)=\frac{对边}{斜边}$

$\cos(\theta)=\frac{邻边}{斜边}$

$\tan(\theta)=\frac{对边}{邻边}$

$\cot(\theta)=\frac{邻边}{对边}$

余弦定理

对于任意三角形，任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。

$c^2 = a^2 + b^2 - 2ab\cos\gamma$

勾股定理

直角三角形的两条直角边的长度的平方和等于斜边长的平方。

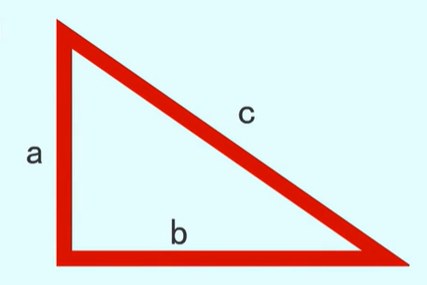
$c^2=a^2+b^2$

已知 $\cos(90^{\circ})=0$，结合余弦定理，可以知道勾股定理是余弦定理的特定情况。

正弦曲线

水平方向和垂直方向同时做正弦运动，就得到了圆周运动。

下面视频展示了从圆中分解出正弦曲线的过程：

标准的正弦曲线函数是 $y=\sin(x)$ ，下图是一个标准的正弦曲线：

与正弦曲线相关的概念有：

周期

周期：从一个顶点到另一个顶点的距离，标准正弦曲线的周期是 $2\pi$

振幅

振幅：从中线（X 轴）到顶点的距离，如上图所示。

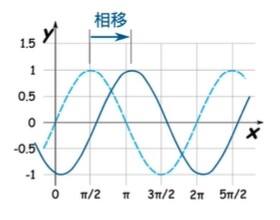
相移

相移：曲线的左右平移，如下图所示。

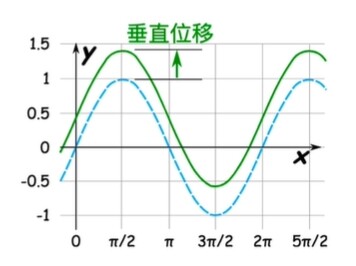
垂直位移

垂直位移：曲线的上下平移，如下图所示。

伸缩变换

下图分别绘制了$y=\sin(x)$、$y=\sin(\frac{1}{2}x)$、$y=\sin(2x)$的图像。

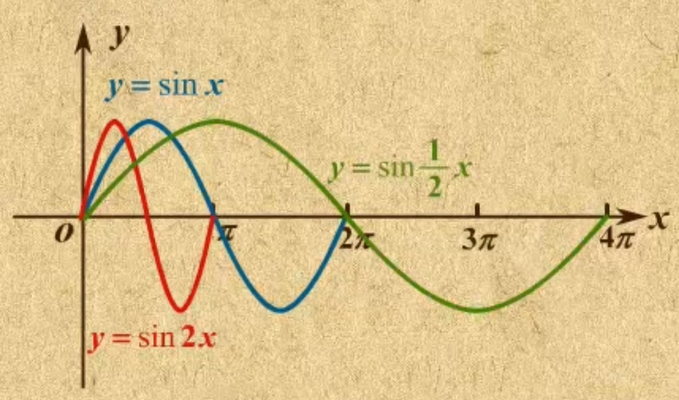
从上图可知，$x$ 所乘以的系数对应曲线周期缩小的倍数。

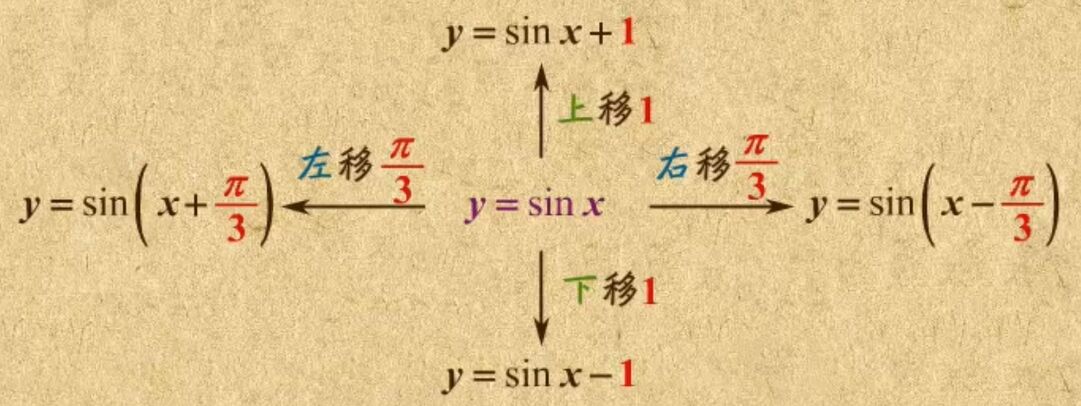
平移变换

正弦曲线的平移变换遵循“左加右减，上加下减”的规则。

实例

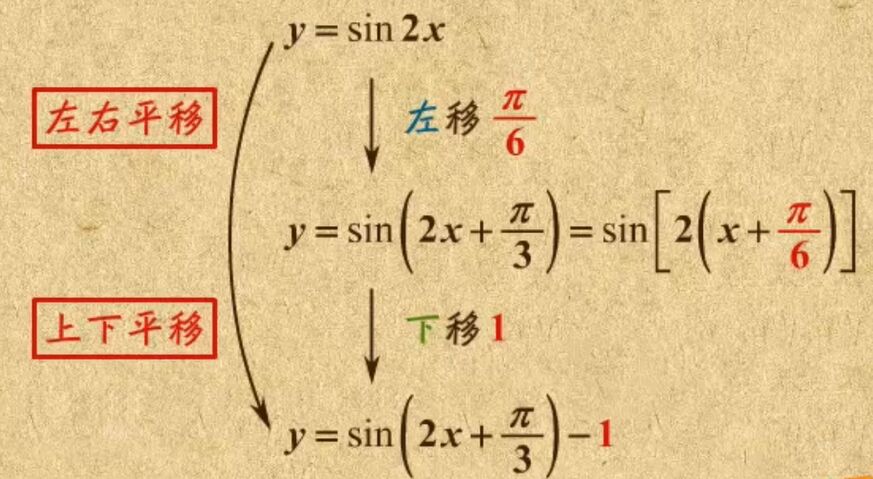
下图展示了从 $y=\sin(2x)$ 变换到 $y=\sin(2x+\frac{\pi}{3})-1$ 的过程。

综合变换

正弦曲线可表示为 $y=A\sin({\omega}x+\varphi)+k$

下图演示了从 $y=\sin(x)$ 变换到 $y=2\sin(2x+\frac{\pi}{4})+1$ 的过程。

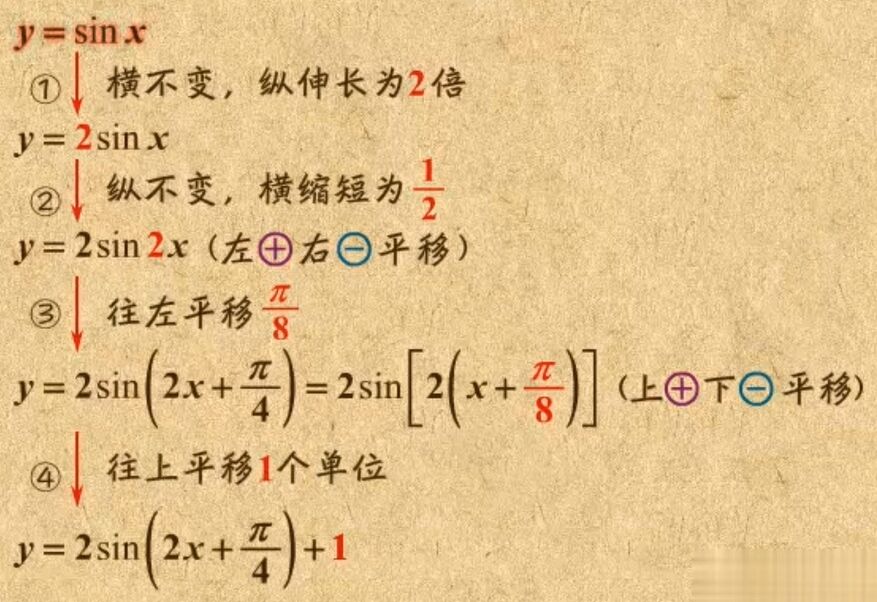
三角函数的值域和公式

常用公式

$\sin^{2}\alpha + \cos^{2}\alpha = 1$

$\frac{\sin\alpha}{\cos\alpha} = \tan\alpha$

$\frac{1}{\cot\alpha} = \tan\alpha$

$\sin(\pi + \alpha) = -\sin(\alpha)$

$\sin(\pi - \alpha) = -\sin(\alpha)$

$\cos(\pi + \alpha) = -\cos(\alpha)$

$\cos(\pi - \alpha) = -\cos(\alpha)$

$\tan(\pi + \alpha) = \tan(\alpha)$

$\tan(\pi - \alpha) = -\tan(\alpha)$

$\cot(\pi + \alpha) = \cot(\alpha)$

$\cot(\pi - \alpha) = -\cot(\alpha)$

$\sin(-\alpha) = -\sin(\alpha)$

$\cos(-\alpha) = \cos(\alpha)$

$\tan(-\alpha) = -\tan(\alpha)$

$\cot(-\alpha) = -\cot(\alpha)$

值域

$\sin(\alpha)$ 和 $\cos(\alpha)$ 值域为 [-1, 1]

$\tan(\alpha)$ 和 $\cot(\alpha)$ 值域为整个实数集

椭圆

椭圆（Ellipse）是平面内到定点 F1、F2 的距离之和等于常数（大于$|F1F2|$）的动点 P 的轨迹，F1、F2 称为椭圆的两个焦点。

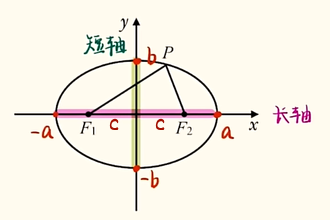
其数学表达式为：

$|PF1|+|PF2|=2a$

两焦点 F1、F2 的距离$|F1F2| = 2c$

椭圆方程式

我们始终用$a$表示长半轴，用$b$表示短半轴，即上图的焦点在 X 轴时，$a$位于 X 轴，若焦点在 Y 轴则$a$位于 Y 轴。

当两个焦点在 X 轴时，标准方程为：$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$

当两个焦点在 Y 轴时，标准方程为：$\frac{y^2}{a^2} + \frac{x^2}{b^2} = 1$

椭圆面积

椭圆面积 $S = \pi ab$

相关公式

$b^2 = a^2 - c^2$

证明如下：

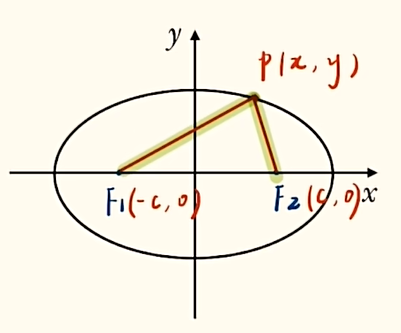
由两点间的距离公式可得：

$|PF1| = \sqrt{(x+c)^2+y^2}$

$|PF2| = \sqrt{(x-c)^2+y^2}$

又因为$|PF1|+|PF2|=2a$，即：

$\sqrt{(x+c)^2+y^2}+\sqrt{(x-c)^2+y^2}=2a$

表达式化简后：

$\sqrt{(x+c)^2+y^2}=2a-\sqrt{(x-c)^2+y^2}$

$(x+c)^2+y^2=(2a-\sqrt{(x-c)^2+y^2})^2$

继续展开和化简，最终可得：

$\frac{x^2}{a^2} + \frac{y^2}{a^2-c^2}=1$

参考椭圆的公式可得：

$b^2 = a^2 - c^2$

椭圆上任意角度点的坐标

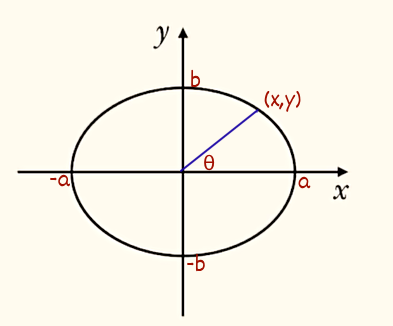
上图焦点位于 X 轴，由椭圆方程式可得：

$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$

由正切函数可得：$y=x\tan(\theta)$

将 $y$ 代入上面表达式可得：

$\frac{x^2}{a^2}+\frac{(x\tan(\theta))^2}{b^2}=1$

最终求得：

$x^2=\frac{a^2b^2}{b^2+a^2(\tan\theta)^2}$

$x$ 可以为正/负值，需要根据角度决定正负。

本文使用latexlive生成数学公式。